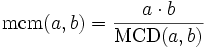In matematica il minimo comune multiplo (mcm) di due interi a e b è il più piccolo intero positivo che è multiplo sia di a che di b. Se non esiste un intero positivo con queste proprietà, cioè se a = 0 o b = 0, allora mcm(a, b) è definito uguale a zero.

Il minimo comune multiplo è uno strumento utile per determinare la somma o sottrazione di due frazioni: in questo caso il denominatore della frazione risultante è il minimo comune multiplo delle due date. Ad esempio, nella somma

il denominatore è mcm(21, 6) = 42.

Se a e b non sono entrambi nulli, il minimo comune multiplo può essere calcolato usando il massimo comun divisore (MCD) di a e b e la formula seguente:

Quindi, l’algoritmo di Euclide per il MCD fornisce anche un veloce algoritmo per il calcolo del mcm. Ritornando all’esempio precedente,

Calcolo efficiente del mcm [modifica]

La formula

è adeguata per calcolare il mcm per piccoli numeri.

Poiché (ab)/c = a(b/c) = (a/c)b, è possibile calcolare il mcm usando la formula precedente in modo più efficiente, dapprima utilizzando il fatto che b/c o a/c sono più semplici da calcolare rispetto al divisione tra il prodotto ab e c: il fatto che c sia multiplo sia di a che di b consente di semplificare completamente il fattore c dalla frazione a/c oppure da b/c, prima di effettuare il prodotto ab.

Allora il mcm si può calcolare o così:

oppure così:

In questo modo, l’esempio precedente diventa:

Anche se i numeri sono grandi e non sono facilmente scomponibili in fattori, il MCD può essere calcolato velocemente usando l’algoritmo di Euclide.

Come ricordarsi di semplificare prima di moltiplicare [modifica]

Il metodo che segue rende impossibile dimenticarsi di semplificare prima di moltiplicare. Verrà illustrato con un esempio: come trovare il mcm(12, 8).

• Si deve ridurre ai minimi termini la frazione avente come numeratore e denominatore i due numeri di cui si deve trovare il minimo comune multiplo:

• Si esegue la "moltiplicazione a croce":

• Il prodotto 12 × 2 = 8 × 3 è il mcm: 24.

Metodo di calcolo alternativo [modifica]

Il teorema fondamentale dell’aritmetica afferma che ogni intero maggiore di 1 può essere scritto in un modo unico come prodotto di fattori primi. I numeri primi possono essere considerati come "atomi" che, combinati insieme, producono un numero composto.

Per esempio:

Il numero composto 90 è costituito da un atomo uguale al numero primo 2, due atomi uguali al numero primo 3 e un atomo uguale al numero primo 5.

Si può usare questo teorema per trovare facilmente il mcm di un gruppo di numeri.

Per esempio: calcolare il mcm(45, 120, 75).

Il mcm è il numero composto da tutti i fattori primi dei numeri dati, presi una sola volta con il massimo esponente. Quindi

Questo è il metodo che di solito viene insegnato nella scuola italiana.

Esempi

• Calcolo di mcm(3, 5, 7 ):

i tre numeri sono primi, quindi

mcm(3,5,7)=3·5·7=105

• Calcolo di mcm(7, 8, 20):

i numeri non primi devono essere scomposti in fattori primi

7=7

8=2·2·2=2³

20=2·2·5=2²·5

allora il mcm risulta

mcm(7,8,20)=7·2³·5=280.

il fattore primo 2 è stato preso con esponente massimo 3.

Analogamente si ragiona se si vuole eseguire il mcm tra espressioni algebriche: si procede alla scomposizione in fattori (monomi, binomi, trinomi…, comunque espressioni algebriche non trasformabili in prodotto di espressioni algebriche di grado inferiore) primi tra loro e si ricava il mcm tra le espressioni algebriche applicando la stessa definizione data per i numeri, ricordando che mcm(4a,bc) non è detto che sia 4abc.

Esempio:

• Calcolo di mcm(2np, (p+q)², 4n²(q+p)³).

Le espressioni sono già indicate come prodotti di espressioni algebriche semplici e allora il loro mcm risulta

mcm(2np, (p+q)², 4n²(q+p)³)=mcm(4,n²,p,(p+q)³)

• Calcolo di mcm(x³, ab(x²-2x+1), (1-x)).

Si ha che

x³= x³

ab(x²-2x+1) = ab(x-1)² = ab(1-x)²

(1-x)= -(x-1).

E quindi il mcm in questo caso è

mcm(x³, ab(x²-2x+1), (1-x))=mcm(ab,x³(1-x)²) =mcm(ab,x³(x-1)²)